Divide and Conquer principle in C Programming
It was a strategy used by British to rule India. Lol...........
Joke apart, Now coming to the right answer:
It is an algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.
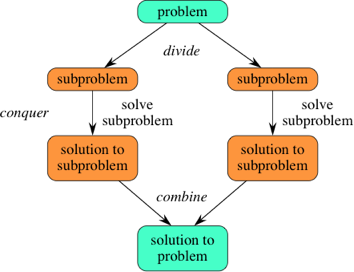
It was strategy used to reduce time complexity of an iterative approach. By using recursion. By splitting the input in to certain equal numbers, e.g dividing into 2 equal halves and applying the same strategy on on those halves which leads to recursion. Thus reducing the complexity. For example merge sort achieving nlogn complexity using dividing and conquer approach.
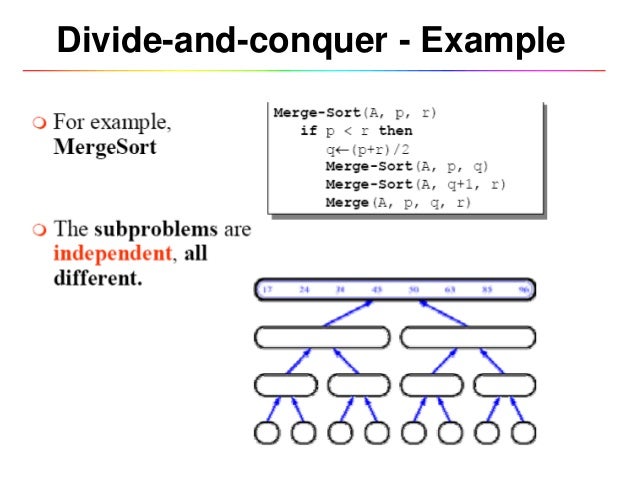
Example Program:
#include < stdio.h >
int arr[8]={1, 2, 3, 4, 5, 6, 7, 8};
int main()
{
int i;
merge_sort(arr, 0, 7);
printf("Sorted array:");
for(i = 0; i < 8; i++)
printf("%d", arr[i]);
return 0;
}
int merge_sort(int arr[],int low,int high)
{
printf("\nmerge_sort initialization\n");
int mid;
if(low < high)
{
mid = (low + high) / 2;
// Divide and Conquer
merge_sort(arr, low, mid);
printf("\n merge_sort first\n");
merge_sort(arr, mid + 1, high);
printf("\n merge_sort second\n");
// Combine
merge(arr, low, mid, high);
printf("\nmerging\n");
}
return 0;
}
int merge(int arr[], int l, int m, int h)
{
int arr1[10], arr2[10];
int n1, n2, i, j, k;
n1 = m - l + 1;
n2 = h - m;
for(i = 0; i < n1; i++)
arr1[i] = arr[l + i];
for(j = 0; j < n2; j++)
arr2[j] = arr[m + j + 1];
arr1[i] = 9999;
arr2[j] = 9999;
i = 0;
j = 0;
for(k = l; k < = h; k++)
{
if(arr1[i] < = arr2[j])
arr[k] = arr1[i++];
else
arr[k] = arr2[j++];
}
return 0;
}
It was a strategy used by British to rule India. Lol...........
Joke apart, Now coming to the right answer:
It is an algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.

It was strategy used to reduce time complexity of an iterative approach. By using recursion. By splitting the input in to certain equal numbers, e.g dividing into 2 equal halves and applying the same strategy on on those halves which leads to recursion. Thus reducing the complexity. For example merge sort achieving nlogn complexity using dividing and conquer approach.

Example Program:
#include < stdio.h >
int arr[8]={1, 2, 3, 4, 5, 6, 7, 8};
int main()
{
int i;
merge_sort(arr, 0, 7);
printf("Sorted array:");
for(i = 0; i < 8; i++)
printf("%d", arr[i]);
return 0;
}
int merge_sort(int arr[],int low,int high)
{
printf("\nmerge_sort initialization\n");
int mid;
if(low < high)
{
mid = (low + high) / 2;
// Divide and Conquer
merge_sort(arr, low, mid);
printf("\n merge_sort first\n");
merge_sort(arr, mid + 1, high);
printf("\n merge_sort second\n");
// Combine
merge(arr, low, mid, high);
printf("\nmerging\n");
}
return 0;
}
int merge(int arr[], int l, int m, int h)
{
int arr1[10], arr2[10];
int n1, n2, i, j, k;
n1 = m - l + 1;
n2 = h - m;
for(i = 0; i < n1; i++)
arr1[i] = arr[l + i];
for(j = 0; j < n2; j++)
arr2[j] = arr[m + j + 1];
arr1[i] = 9999;
arr2[j] = 9999;
i = 0;
j = 0;
for(k = l; k < = h; k++)
{
if(arr1[i] < = arr2[j])
arr[k] = arr1[i++];
else
arr[k] = arr2[j++];
}
return 0;
}

Cougar Conquer Case in UAE, Aluminum ATX Mid-Tower Case in UAE, ATX Gaming Computer Case in UAE
ReplyDeletehttps://pcdubai.com/cougar-conquer/
Cougar Conquer Case in UAEE, Safe Shopping Multiple Payment Options Express Delivery PC Dubai Moneyback Guarantee.
1633929342282-7